In this class, we will learn what the derivative of trigonometric sine function is, and discusses the process of finding the derivative of the sine function sin(x), including a proof using the First Principle of Calculus.

Derivative of the Sin x

The derivative of \({\ sin(x) }\) with respect to \({\ x }\) is \({\ cos(x) }\).

(d/dx) sin(x) == cos(x)

or

\({\ \\(sin(x))' = cos(x) }\)

Thus, if \({\ f(x) = sin(x) }\), then \({\ f'(x) = cos(x) }\) .

The derivative of the sine function is a fundamental concept in calculus. It is important for solving problems involving trigonometric functions.

Graph of Sin x and Derivative of Sin x

The following is the graph of sin(x) in red color.

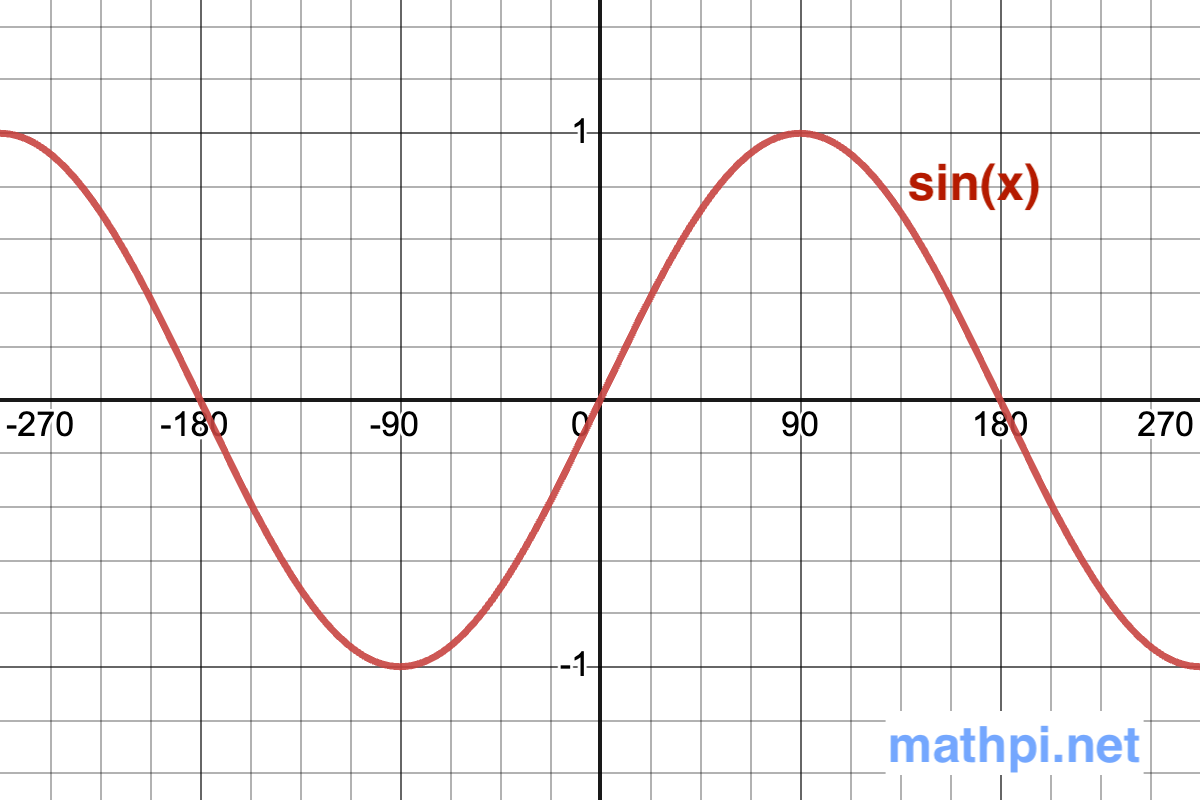
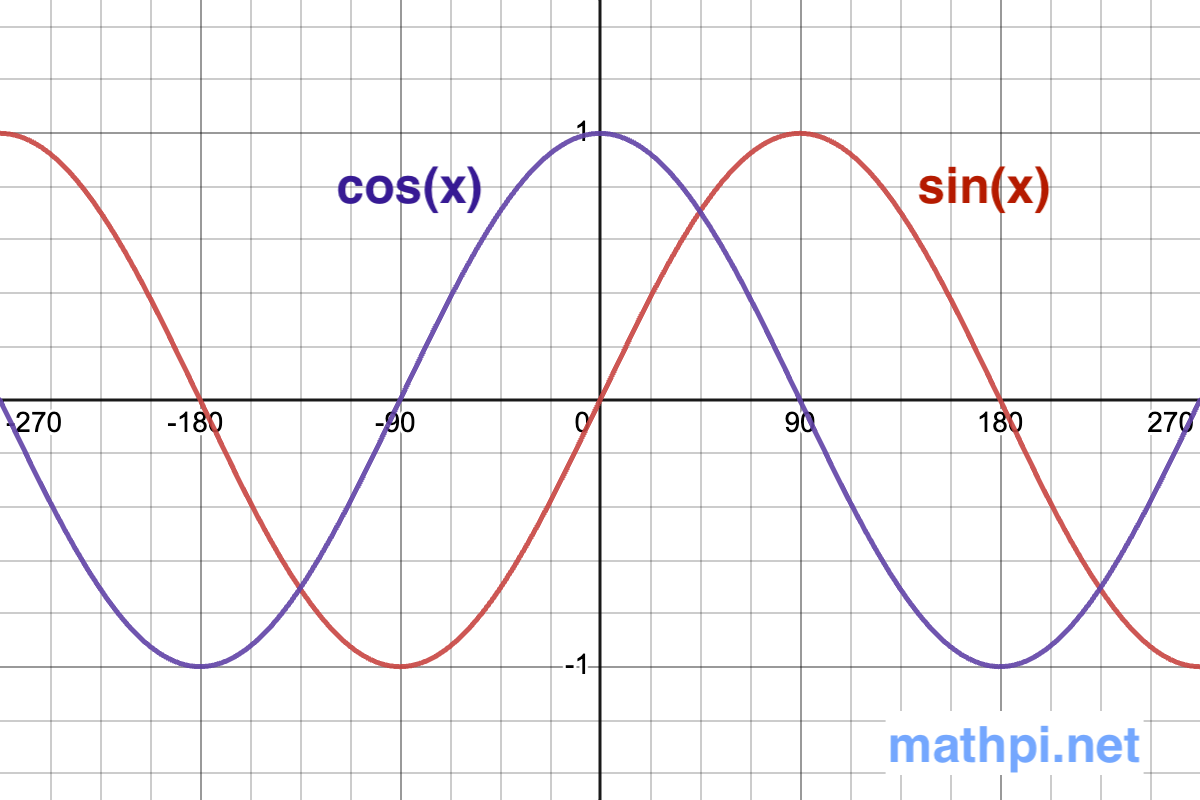
The following is the graph of sin(x) in red color, and the derivative of sin(x) i.e., cos(x) in blue color.

Proof of Derivative of sin(x): (d/dx) sin(x) == cos(x)

The First Principle of Calculus, also known as the limit definition of the derivative, can be used to derive the derivative of sin(x).

The principle states that:

\({\ \\f'(x) = lim_{h \to 0} \frac{f(x+h) - f(x)}{h} }\)

Applying this definition to sin(x), we get:

\({\ \\(sin(x))' = lim_{h \to 0} \frac{sin(x+h) - sin(x)}{h} }\) ...1

The trigonometric identity for sin(x + h) is

\({\ sin(x + h) = sin(x)cos(h) + cos(x)sin(h) }\) ...2

Substitute the value of sin(x+h) from 2 in equation 1

\({\ \\(sin(x))' = lim_{h \to 0} \frac{sin(x)cos(h) + cos(x)sin(h) - sin(x)}{h} }\)

\({\ \\(sin(x))' = lim_{h \to 0} \frac{-sin(x)(1 - cos(h)) + cos(x)sin(h)}{h} }\)

\({\ \\(sin(x))' = lim_{h \to 0} \frac{-sin(x)(1 - cos(h))}{h} + lim_{h \to 0} \frac{cos(x)sin(h)}{h} }\)

Bring out the terms that does not contain the limit variable h.

\({\ \\(sin(x))' = -sin(x) lim_{h \to 0} \frac{(1 - cos(h))}{h} + cos(x) lim_{h \to 0} \frac{sin(h)}{h} }\) ...3

The trigonometric identity for 1 - cos(h) is: 1 - cos(h) == 2*sin^2 (h/2) ...4

Also \({\ lim_{x \to 0} \frac{sin(x)}{x} } = 1 \) ...5

Substitute the value of 1 - cos(h) from 4 and the value of \({\ lim_{h \to 0} \frac{sin(h)}{h} } \) from equation 5 into the equation 3

\({\ \\(sin(x))' = -sin(x) lim_{h \to 0} \frac{(2sin^2(h/2))}{h} + cos(x) × 1 }\)

\({\ \\(sin(x))' = -sin(x) lim_{h \to 0} \frac{(2sin^2(h/2))}{h} + cos(x) }\)

\({\ \\(sin(x))' = -sin(x) × [lim_{h \to 0} \frac{(sin(h/2))}{h/2} × (sin(h/2))] + cos(x) }\)

\({\ \\(sin(x))' = -sin(x) × [lim_{h \to 0} \frac{(sin(h/2))}{h/2} × lim_{h \to 0} (sin(h/2))] + cos(x)}\)

We already know that \({\ lim_{x \to 0} \frac{sin(x)}{x} } = 1 \), and \({\ lim_{x \to 0} {sin(x)} } = 0 \)

\({\ \\(sin(x))' = -sin(x) × [1 × 0] + cos(x) }\)

\({\ \\(sin(x))' = -sin(x) × 0 + cos(x) }\)

\({\ \\(sin(x))' = 0 + cos(x) }\)

\({\ \\(sin(x))' = cos(x) }\)

Therefore, the derivative of sin(x) is cos(x), as proven using the First Principle of Calculus.

(d/dx) sin(x) == cos(x)

We have proved the equation for the derivative of sin(x).